- マインスイーパー
- マインスイーパーのこつ
- P助のマインスイーパ塾|角の1、端の2、壁の3
- P助のマインスイーパ塾|1・2の法則
- P助のマインスイーパ塾|1・2・1の法則
- P助のマインスイーパ塾|1・2・2・1の法則
- P助のマインスイーパ塾|壁1・1の法則
- P助のマインスイーパ塾|かぶりの法則
- P助のマインスイーパ塾|1・4の法則
- P助のマインスイーパ塾|2・5の法則
- P助のマインスイーパ塾|3・6の法則
- P助のマインスイーパ塾|4・7の法則
- P助のマインスイーパ塾|角1・3・1の法則
- P助のマインスイーパ塾|角2・2・2の法則
- P助のマインスイーパ塾|仮定矛盾確定の法則
- P助のマインスイーパ塾|まとめ
- 2つの内1つに旗が立つ場合の対応
- マインスイーパーのこつ|プロマインスイーパー完全攻略解説動画
- マインスイーパー実戦
- マインスイーパー関連記事
マインスイーパー
マインスイーパーとは
・1980年代に発明された、一人用のコンピュータゲーム。
・マインスイーパともいう。
・地雷除去ゲーム。
・正方形のマスが敷き詰められた長方形のフィールドから構成されている。
・それぞれのマスは開けることができるが、地雷の置かれているマスを開けると負けとなる。
・地雷の置かれていないマスを開けたときは、隣接する8方向のマスのいずれかに地雷がある場合はその個数が表示される。
・隣接するマスに地雷が置かれていないときは、それらが自動的に開けられる。
・地雷の置かれていないマスをすべて開ければ勝ちとなる。
・地雷が置かれていると思われるマスに旗を立てることができる。これは盤面を簡略化し他の地雷の位置の推測を容易にする。
マインスイーパーの一部実装 時間短縮
・表示された個数と同じだけの旗を立てたマスで中ボタンをクリック(または左右のボタンを同時に押下)すると、隣接する開けられていないマスを一気に開けることができる。
・このとき開けられたマスに地雷が置かれていれば、ゲーム終了となる。
・地雷にマークしたあと右ボタンを押下したまま移動することを許している。これによってプレイヤーは短い時間で大きな区域を開けるために、マウスの右ボタンをドラッグしながらいくつかの数字のマスを左クリックすることができる。
マインスイーパーのこつ
マインスイーパーのこつ|初級
・【初心者向け】マインスイーパで遊ぼう【基本ルールと解き方】
・『ちょっとゆっくり解説』マインスイーパーについて解説していくよ
マインスイーパーのこつ|消すより旗を先に立てる
・消すゲームであるため、「消す」を優先しがちだが、消してはダメ意味の「旗」を先に立てた方がよい。
・誤って消すのを防ぐため。
・「旗」を先に立てることにより、「1」の周りで「消す」マスが結果的に増えるため。これは、時間を使って数えれば、「2」以上の数の周りを消すことができる。
マインスイーパーのこつ|確率50%しかない場合はすぐに消す
・後回しにすることが時間の無駄であるため、確率50%しかない場合はすぐに消す。
マインスイーパーのこつ|3つおき確定
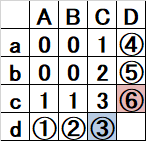
■①か②に地雷がある。
■Bcが「1」であるため、③に地雷が無い。
■④か⑤に地雷がある。
■Cbが「2」であるため、⑥に地雷が有る。
・【単発】マインスイーパテクニック ~3つおき確定のテクニック~
P助のマインスイーパ塾|角の1、端の2、壁の3
角の1
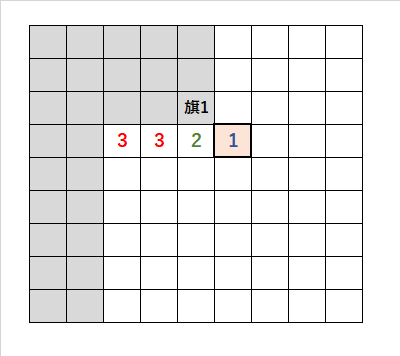
・赤いマスの「1」に注目すると、角にある「旗1」を立てることができる。
端の2
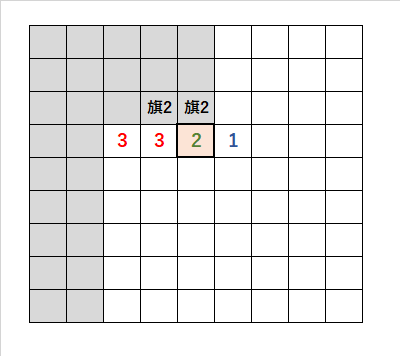
・赤いマスの「2」に注目すると、端にある「旗2」を立てることができる。
壁の3
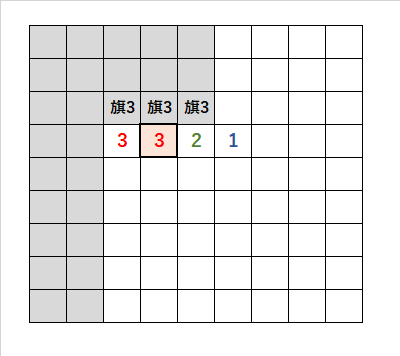
・赤いマスの「3」に注目すると、壁にある「旗3」を立てることができる。
P助のマインスイーパ塾|1・2の法則
1・2の法則|説明
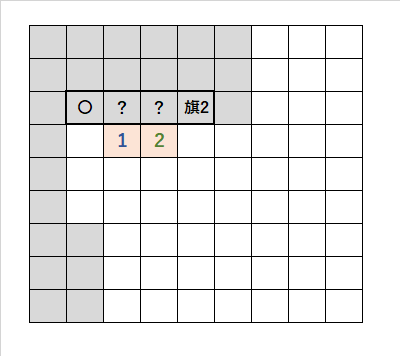
・「1・2」の並び順で、「灰色の太いマス目」に注目する。
・「2」に接していない「1」の「斜め上のマス目」は、開けるので「〇」。
・「2」に接している「1」の「上、斜め上のマス目」は、どちらかに爆弾で「?」。
・「2」に接しているが「1」に「接していないマス目」は、爆弾で「旗2」。
1・2の法則|場合分けによる根拠
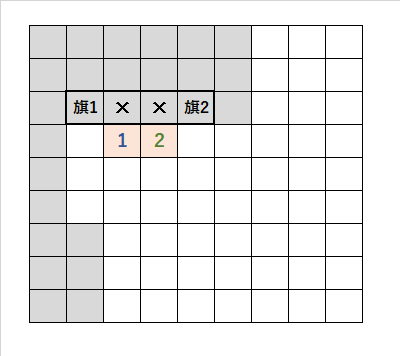
・「2」に接していない「1」の「斜め上のマス目」に、「旗1」を立てると、「旗2」が2本立てれない。矛盾する。
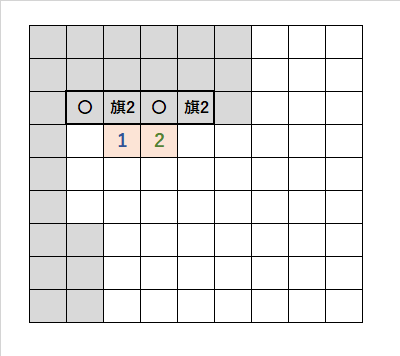
・「2」に接していない「1」の「斜め上のマス目」を、開ける「〇」と、成立する。
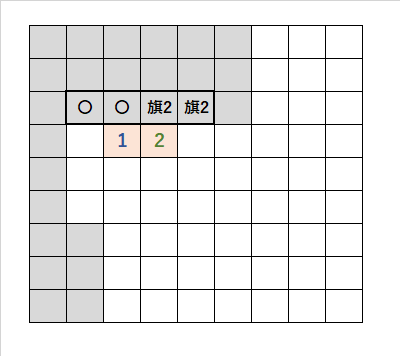
・「2」に接していない「1」の「斜め上のマス目」を、開ける「〇」と、これも成立する。

・したがって、上の図が成立する。
P助のマインスイーパ塾|1・2・1の法則
1・2・1の法則|説明
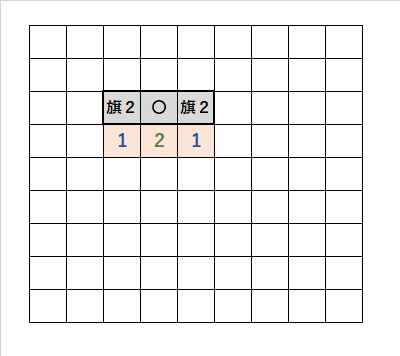
・「1・2・2・1」の並び順で、「灰色の太いマス目」に注目する。
・「1」の「上のマス目」は、爆弾で「旗2」が2つ。
・「2」の「上のマス目」は、開けるので「〇」。
1・2・1の法則|場合分けによる根拠
・「1」の「上のマス目」を開けると、「旗2」が2本立てれない。矛盾する。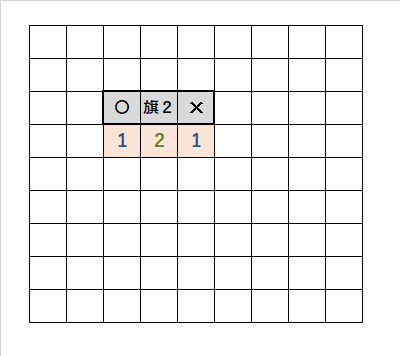
P助のマインスイーパ塾|1・2・2・1の法則
1・2・2・1の法則|説明
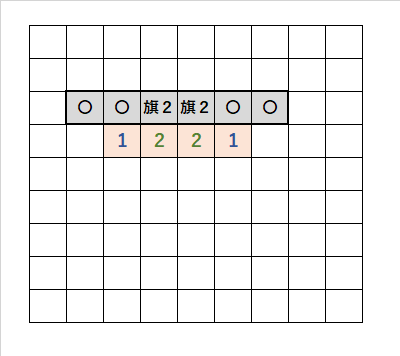
・「1・2・2・1」の並び順で、「灰色の太いマス目」に注目する。
・「1」の「2に接してないマス目」、「1」の「上のマス目」は開けるので「〇」。
・「2」の「上のマス目」は、爆弾で「旗2」が2つ。
1・2・2・1の法則|場合分けによる根拠
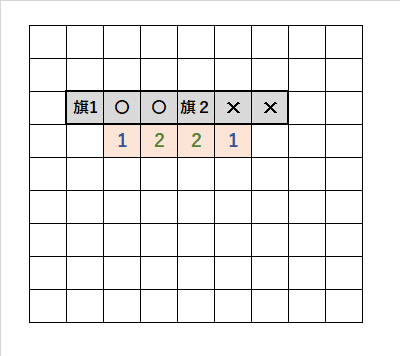
・「1」の「2に接してないマス目」に「旗1」を立てると、「旗2」が2本立てれない。矛盾する。
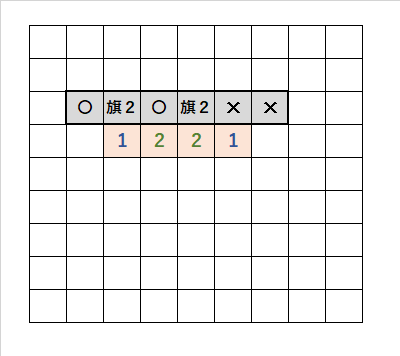
・「1」の「上のマス目」に「旗2」を立てると、右側の「旗2」が2本立てれない。矛盾する。
P助のマインスイーパ塾|壁1・1の法則
壁1・1の法則|説明
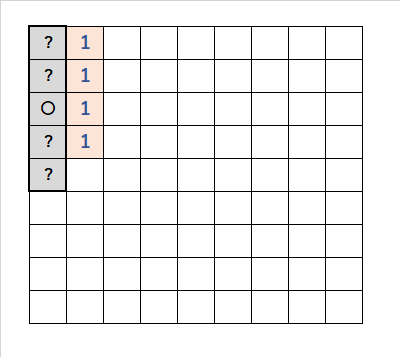
・「1・1・1・1」の並び順で、「灰色の太いマス目」に注目する。
・「1」の「壁から3番目のマス目」は、開けるので「〇」。
・「1」の「他の灰色の太いマス目」は、爆弾の可能性。
壁1・1の法則|場合分けによる根拠
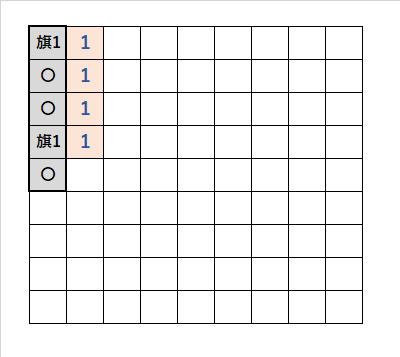
・「1」の「壁から1番目のマス目」に「旗1」を立てると、「壁から2、3、5番目のマス目」は開けるので「〇」。
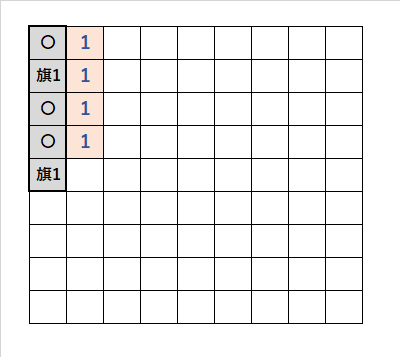
・「1」の「壁から2番目のマス目」に「旗1」を立てると、「壁から1、3、4番目のマス目」は開けるので「〇」。
・したがって、いずれの場合でも、「1」の「壁から3番目のマス目」は、開けるので「〇」。
P助のマインスイーパ塾|かぶりの法則
かぶりの法則|説明
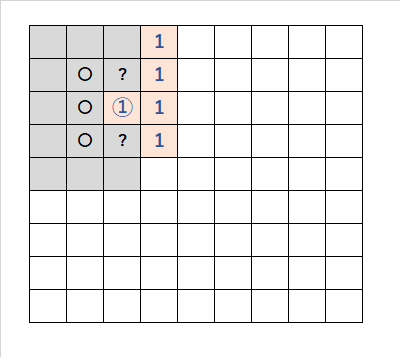
・「1・1・1・1」の並び順で、『壁1・1』の法則により、開けて「①」が出た状況。この状況は、かなり搬出するので、覚えておいた方がよい。
・「①」の「上」か「下」のどちらかの「?」に「1」が入る。
・したがって、「①」に接する「〇」は、開くことができる。
・応用で、「①」の周辺の2つに一つが爆弾があると推察できる場合、他の「①」の周辺は全て開けることができる。開けるものが無い場合、この方法は使える。
P助のマインスイーパ塾|1・4の法則
1・4の法則|説明
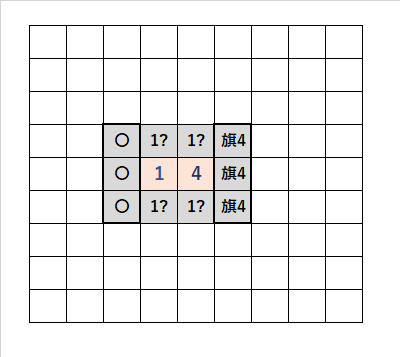
・「1」に注目すると、「1?」の候補が4つのどれか1つになる。
・「4」に注目すると、「旗4」の3つは確定する。残りの1つは「1?」のどれかである。
・「1」に注目すると、「1?」の候補が4つのどれか1つになるため、他に「1」に接する3つの「〇」を開けることができる。
・「1」と「4」の差が3つであるときに成立する。
P助のマインスイーパ塾|2・5の法則
2・5の法則|説明
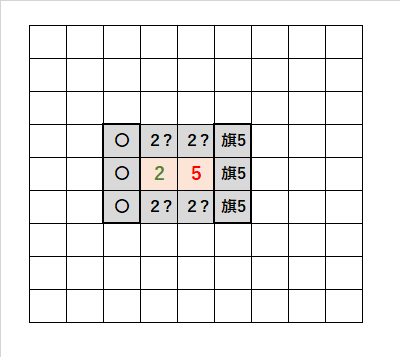
・「2」に注目すると、「2?」の候補が4つのどれか2つになる。
・「5」に注目すると、「旗5」の3つは確定する。残りの2つは「2?」のどれかである。
・「2」に注目すると、「2?」の候補が4つのどれか2つになるため、他に「1」に接する3つの「〇」を開けることができる。
・「2」と「5」の差が3つであるときに成立する。
P助のマインスイーパ塾|3・6の法則
3・6の法則|説明
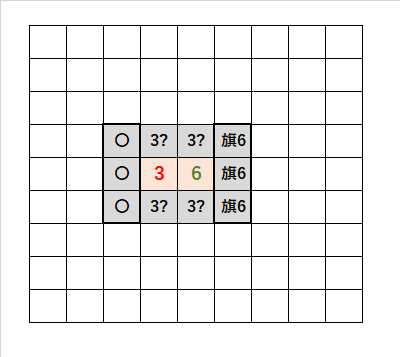
・「3」に注目すると、「3?」の候補が4つのどれか3つになる。
・「6」に注目すると、「旗6」の3つは確定する。残りの3つは「3?」のどれかである。
・「3」に注目すると、「3?」の候補が4つのどれか3つになるため、他に「1」に接する3つの「〇」を開けることができる。
・「3」と「6」の差が3つであるときに成立する。
P助のマインスイーパ塾|4・7の法則
4・7の法則|説明
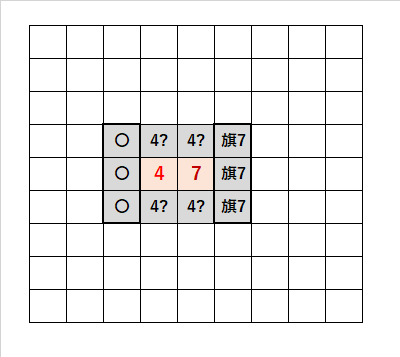
・「4」に注目すると、「4?」の候補が4つになる。
・「7」に注目すると、「旗7」の3つは確定する。残りの4つは「4?」である。
・「4」に注目すると、「4?」の候補が4つになるため、他に「1」に接する3つの「〇」を開けることができる。
・「4」と「7」の差が3つであるときに成立する。
P助のマインスイーパ塾|角1・3・1の法則
角1・3・1の法則|説明
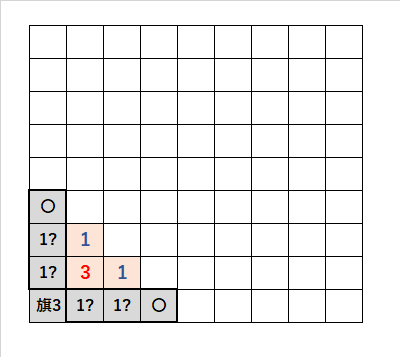
・「3」に注目すると、理論上、「旗3」は確定する。
・「1」に注目すると、「3」に接するマスのどちらかを「1?」にすべき。
・「1」に注目すると、「3」に接しないマスは、「〇」を開けることができる。
・「3」は数が大きいので、角は「旗」と覚えておく。
P助のマインスイーパ塾|角2・2・2の法則
角2・2・2の法則|説明
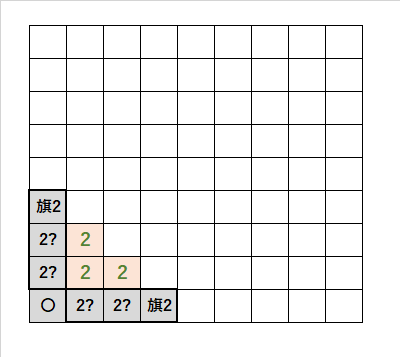
・「2」に注目すると、理論上、「旗2」は確定する。
・「2」に注目すると、「2」の左のマスのどちらかを「2?」にすべき。
・「2」に注目すると、2つの「2」に接しないマスは、「〇」を開けることができる。
・「2」は数が小さいので、角は「〇」と覚えておく。
角2・2・2の法則|勘違いの説明
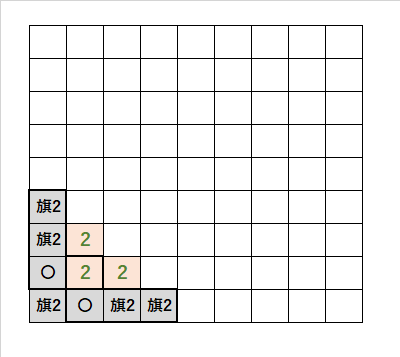
・角に「旗2」を入れると、残りの4つの「旗2」が決まりそうになる。
・しかしながら、角の「2」に接する「旗2」が3つになる。矛盾する。
・「2」は数が小さいので、角は「〇」と覚えておく。
P助のマインスイーパ塾|仮定矛盾確定の法則
・手詰まりになった場合、「仮の旗」を立てていく。
・矛盾が生じた場合、「仮の旗」は誤りであるため、「〇」扱いで開ける。
・詳細は、仮定矛盾確定を参照。
P助のマインスイーパ塾|まとめ
■「角の1」「端の2」「壁の3」、端から解く
■1・2の法則、1・2・1の法則、1・2・2・1の法則
■壁1・1の法則
■かぶりの法則
■1・4の法則、2・5の法則、3・6の法則(3差の法則)
■角1・3・1の法則、角2・2・2の法則
■仮定矛盾確定
【引用して整理しました。敬意を表します。】
2つの内1つに旗が立つ場合の対応
2つの内1つに旗が立つ場合
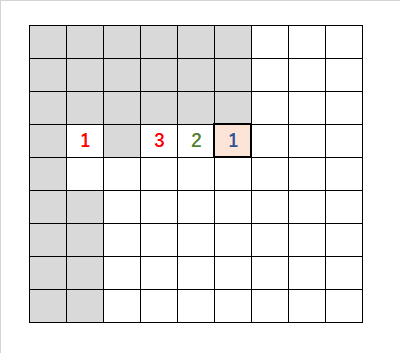
・色付きの「角の1」に注目する。
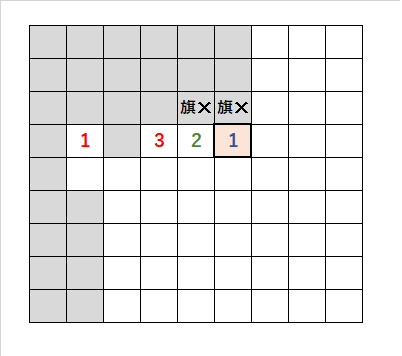
・色付きの「角の1」の、上のマスか、左上のマスのどちらかに旗が立つ。
・「旗✕」は、どちらかに旗が立つことを表している。
2つの内1つに旗が立つ場合、他のマスを考える
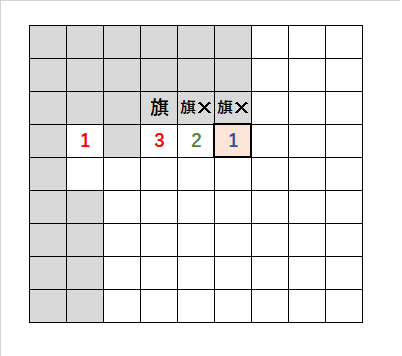
・「旗✕」の下の「2」に注目する。
・「2」の残り1つの旗が「3」の上に立つ。
2つの内1つに旗が立つ場合、さらに他のマスを考える
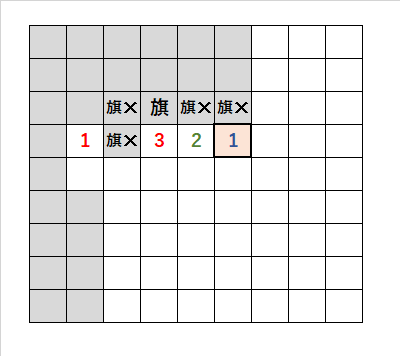
・旗の下の「3」に注目する。
・「3」の、左上のマスか、左のマスのどちらかに旗が立つ。
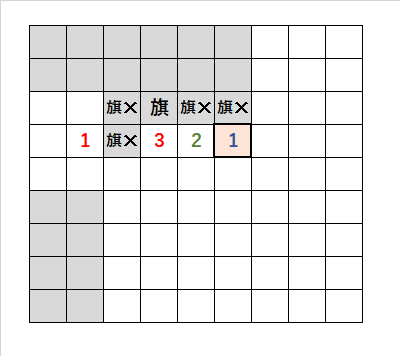
・一番左の「1」に注目する。
・「3」の、左上のマスか、左のマスのどちらかに旗が立つため、他の「1」の周囲は全て開けることができる。
マインスイーパーのこつ|プロマインスイーパー完全攻略解説動画
・プロマインスイーパーによる初心者・中級者・上級者向けの完全攻略解説動画【プロ】
マインスイーパー実戦
マインスイーパー実戦|場所
・OCNトップページ に行き、会員IDでログインする。
・gooゲーム > パズル > マインスイーパCOMBO を選択する。
・毎日、dポイントの抽選券を貯めている。
・3回爆弾を爆発させると、ゲームオーバー。

マインスイーパー実戦|抽選券履歴
マインスイーパー実戦|dポイント当選一覧

マインスイーパー実戦|dポイント当選結果|当初
・LEVEL5を1回につき、+2~+5ポイント。
・1日3回で平均+9ポイント。
・100ポイントで抽選券100枚になり、1回くじが引ける。
・くじの結果は、5等で1ポイント。
マインスイーパー実戦|dポイント当選結果|習熟後
・LEVEL5を1回につき、+5ポイント。
・1日3回で+15ポイント。
・100ポイントで抽選券100枚になり、1回くじが引ける。
・くじの結果は、5等で1ポイントが3回あった。→dポイントが3ポイントです。